My previous post-compress prompt has introduced the way of compression to reduce costs. Recently, I watched the video of HungyiLee about FrugalGPT[1]. In the paper[1], three methods are summaried which can be used to use LLM apis cheaply and efficiently.
The three methods has been shown in the picture below:
- [1] Prompt adaptation: prompt selection + query concatenation
- [2] LLM approximation: Completion cache + Model fine-tuning
- [3] LLM cascade
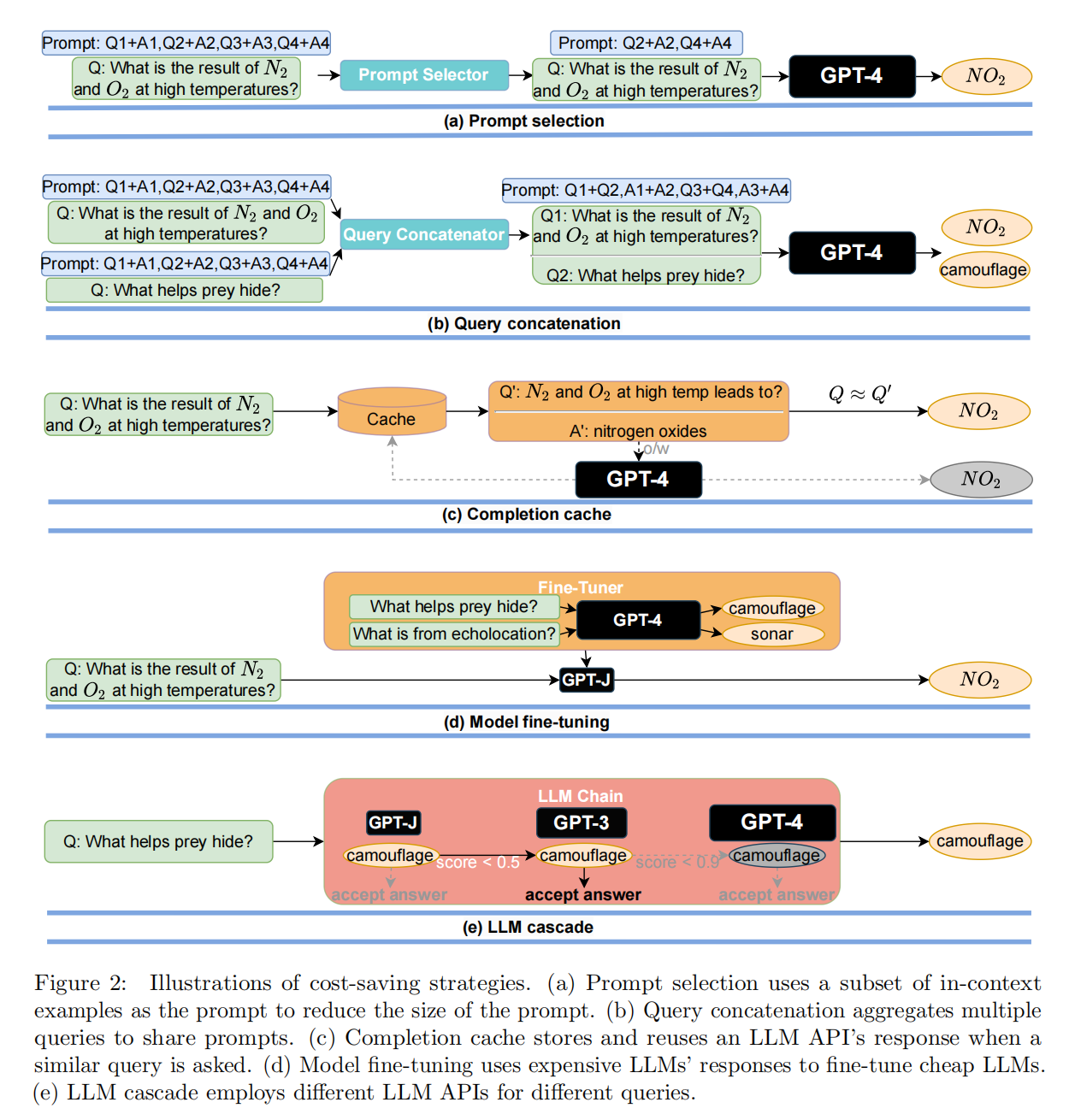
In practice, Combining approaches within and across different strategies can lead to further cost reduction and performance enhancement.
The most interesting part for me is LLM cascade. It use mutiple LLM apis and find the best strategy to save the cost and even improve the performance.
LLM cascade consists of a generation scoring function and a LLM router. The scoring function is a DistilBERT tailored to regression. The LLM router is a LLM list which iteratively invokes the ith API in the list to obtain an answer. The query and answer are feed into scoring function. It returns the generation if the score is higher than a threshold, and queries the next service otherwise.
The problem of finding the best strategy is modeling as an optimization problem as below:
It is a Mixed-integer optimization problem, also known as mixed-integer linear programming (MILP) problems, which involve a combination of continuous and discrete decision variables. In these problems, some variables are allowed to take on only integer values, while others can take on continuous values.
The paper briefly introduced a specialized way to address the issue:
- (i) prunes the search space by ignoring any list of LLMs with small answer disagreement
- (ii) approximates the objective by interpolating it within a few samples.
This method inspires me that: is it possible to train a model that works both scoring function and router?
